Walkthrough

Eager to get started? This page gives a good introduction in how to get started with bigger.

First, make sure that:

• bigger is installed
• bigger is up-to-date

Let’s get started with some simple examples.

Getting a mapping class group

Begin by importing bigger:

>>> import bigger

Now, let’s use the bigger.load.biflute method to load a big mapping class group:

>>> S = bigger.load.biflute()

This builds the mapping class group of the two-ended, infinitely-punctured surface of genus zero.

Laminations

A lamination is specified by a function that returns the number of times that it intersects each edge of the underlying triangulation. As usual, if a lamination has \(k\) components that are parallel to an edge then their intersection is \(-k\). We can create a Lamination by giving a dictionary to the underlying triangulation of the mapping class group. This dictionary maps some of the triangulations edges to the weight assigned to them by the lamination:

>>> c = S.triangulation({1: -1})
>>> c
Lamination 1: -1
>>> c(1), c(3), c(10000), c(-22)
1, 0, 0, 0

Of course, many laminations do not have finite support and so cannot be specified this way. More generally, we can pass a weight function to the mapping class groups underlying triangulations:

>>> a = S.triangulation(lambda e: -1 if e >= 0 and e % 2 == 1 else 0)
>>> a(0), a(1), a(2), a(3)
(0, -1, 0, -1)
>>> a
Infinitely supported lamination 0: 0, -1: 0, 1: -1, -2: 0, 2: 0, -3: 0, 3: -1, -4: 0, 4: 0, -5: 0 ...

By default this assumes that the lamination is supported by all of the triangulation. If we know better then we can also provide an iterator over the support of the lamination:

>>> from itertools import count
>>> a = S.triangulation(
... lambda e: -1 if e >= 0 and e % 2 == 1 else 0,
... support=lambda: (2*i + 1 for i in count()))
>>> a
Infinitely supported lamination 1: -1, 3: -1, 5: -1, 7: -1, 9: -1, 11: -1, 13: -1, 15: -1, 17: -1, 19: -1 ...

Mapping Classes

A mapping class group comes with a number of mapping classes. We can build a mapping class from these:

>>> h = S('a_0.a_0')

We can compute the image of a lamination under a mapping class:

>>> h(c)
Lamination 1: 1, 2: 2

And, since these laminations have finite support and known, we can test whether two such laminations are equal:

>>> S('a_1')(c) == c
True

We can even compute the image of infinitely supported laminations:

>>> h(a)
Infinitely supported lamination 1: 1, 2: 2, 5: -1, 3: -1, 2: 2, 2: 2, 1: 1, 2: 2, 2: 2, 1: 1 ...

Of course, in this case we cannot tell whether two such laminations are equal (or even equal to themselves):

>>> a == a
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
  File "/bigger/decorators.py", line 52, in inner
    raise ValueError(f"{function.__name__} requires the lamination be finitely supported")
ValueError: __eq__ requires the lamination be finitely supported

Visualisations

It’s often hard to visualise or keep track of what is going on on these surfaces. To help with this, bigger can create pictures of laminations on parts of the surface:

>>> L = S.triangulation(lambda edge: 1 if edge % 3 != 2 else 0)
>>> L = S('a.a{n > 1}.a{n > 1}')(L)
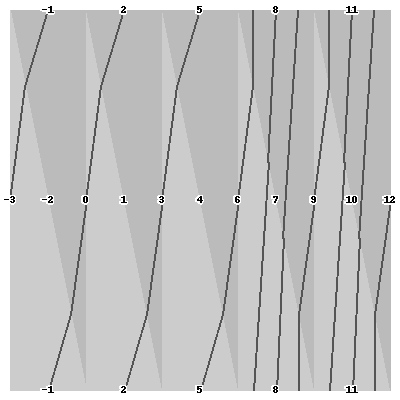
>>> L.draw([-2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11])

This is a pillow Image object and so if you are running bigger within a jupyter notebook it will be automatically rendered in your browser.

If not then you may need to use its show() method to write the image to a temporary file and open it in your image viewer:

>>> L.draw([-2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]).show()

As well as the collection of edges to draw the lamination around, the draw() method supports a number of optional arguments. This includes labels to place on the edges in the picture as well as the size of the image to produce:

>>> L.draw([-2, -1, 3, 4, 5, 6, 7, 8, 9], label='weight', w=800)

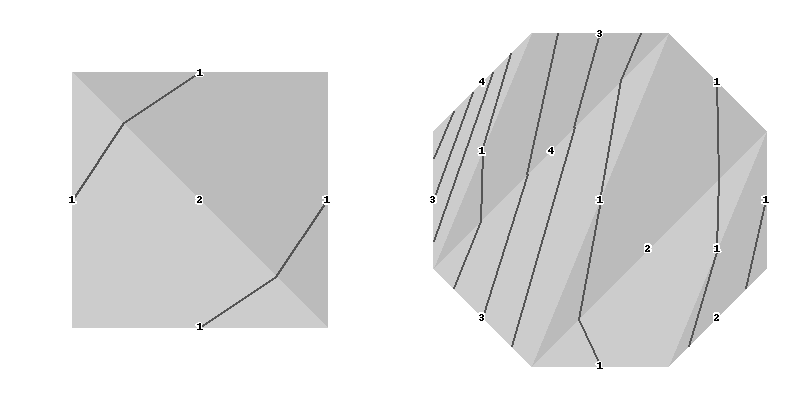
Importantly, the mapping class group provides a standard way of laying out its underlying triangulation:

>>> L.draw([-2, 0, 1, 3, 4, 6, 7, 9, 10], layout=S, label='edge')

Operations on mapping classes

Bigger also allows us to compose together or take powers of existing mapping classes:

>>> g = h * S('b_1')
>>> g(c)
Lamination 1: 2, 2: 3, 3: 1, 4: 2, 6: 2, 7: 1, 8: 1
>>> (g**2)(c)
Lamination 1: 5, 2: 6, 3: 3, 4: 4, 6: 4, 7: 2, 8: 2

Building new mapping classes

Bigger can create new mapping classes by Dehn twistings about a (multi)curve:

>>> twist = S.triangulation({1: 1, 2: 1}).twist()
>>> twist(c), (twist * twist)(c), (twist**3)(c)
(Lamination 2: 1, Lamination 1: 1, 2: 2, Lamination 1: 2, 2: 3)

It can even handle multicurves with infinitely many components:

>>> v = S.triangulation(lambda e: 1 if e % 3 != 0 else 0)
>>> v.twist()(a)
Infinitely supported lamination 2: -1, 2: -1, 2: -1, 3: -1, 4: 1, 4: 1, 4: 1, 8: -1, 8: -1, 8: -1 ...